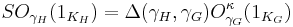Fundamental lemma (Langlands program)

In the theory of automorphic forms, an area of mathematics, the fundamental lemma relates orbital integrals on a reductive group over a local field to stable orbital integrals on its endoscopic groups. It was conjectured by Langlands (1983) in the course of developing the Langlands program. The fundamental lemma was proved by Gérard Laumon and Ngô Bảo Châu in the case of unitary groups and then by Ngô for general reductive groups, building on a series of important reductions made by Jean-Loup Waldspurger to the case of Lie algebras. Time magazine placed Ngô's proof on the list of the "Top 10 scientific discoveries of 2009".[1] In 2010 Ngô was awarded the Fields medal for this proof.

Contents

Motivation and history

Robert Langlands outlined a strategy for proving local and global Langlands conjectures using the Arthur–Selberg trace formula, but in order for this approach to work, the geometric sides of the trace formula for different groups must be related in a particular way. This relationship takes the form of identities between orbital integrals on reductive groups G and H over a nonarchimedean local field F, where the group H, called an endoscopic group of G, is constructed from G and some additional data.

The first case considered was G = SL2 (Labesse and Langlands, 1979). Langlands and Diana Shelstad then developed the general framework for the theory of endoscopic transfer and formulated specific conjectures. However, during the next two decades only partial progress was made towards proving the fundamental lemma.[2][3] Harris called it a "bottleneck limiting progress on a host of arithmetic questions".[4] Langlands himself, writing on the origins of endoscopy, commented:

“ ... it is not the fundamental lemma as such that is critical for the analytic theory of automorphic forms and for the arithmetic of Shimura varieties; it is the stabilized (or stable) trace formula, the reduction of the trace formula itself to the stable trace formula for a group and its endoscopic groups, and the stabilization of the Grothendieck–Lefschetz formula. None of these are possible without the fundamental lemma and its absence rendered progress almost impossible for more than twenty years.[5] ”

Statement

The fundamental lemma states that an orbital integral O for a group G is equal to a stable orbital integral SO for an endoscopic group H, up to a transfer factor Δ (Nadler 2012):

SO_{\gamma_H}(1_{K_H}) = \Delta(\gamma_H,\gamma_G)O^\kappa_{\gamma_G}(1_{K_G})

where

Approaches

Shelstad (1982) proved the fundamental lemma for archimedian fields.

A paper of George Lusztig and David Kazhdan pointed out that orbital integrals could be interpreted as counting points on certain algebraic varieties over finite fields. Further, the integrals in question can be computed in a way that depends only on the residue field of F; and the issue can be reduced to the Lie algebra version of the orbital integrals. Then the problem was restated in terms of the Springer fiber of algebraic groups.[6] The circle of ideas was connected to a purity conjecture; Laumon gave a conditional proof based on such a conjecture, for unitary groups. Laumon and Ngô then introduced the use of the Hitchin fibration, which is an abstract geometric analogue of the Hitchin system of mathematical physics, as a further technical tool, leading ultimately to a proof of the "function field" case. Waldspurger (2006) showed for Lie algebras that the function field case implies the fundamental lemma over all local fields, and Waldspurger (2008) showed that the fundamental lemma for Lie algebras implies the fundamental lemma for groups. .

Notes

  1. ^ Top 10 Scientific Discoveries of 2009, Time
  2. ^ Kottwitz and Rogawski for U3, Wadspurger for SLn, Hales and Weissauer for Sp4.
  3. ^ Fundamental Lemma and Hitchin Fibration, Gérard Laumon, May 13, 2009
  4. ^ INTRODUCTION TO “THE STABLE TRACE FORMULA, SHIMURA VARIETIES, AND ARITHMETIC APPLICATIONS”, p. 1., Michael Harris
  5. ^ publications.ias.edu
  6. ^ The Fundamental Lemma for Unitary Groups, at p. 12., Gérard Laumon

References

External links